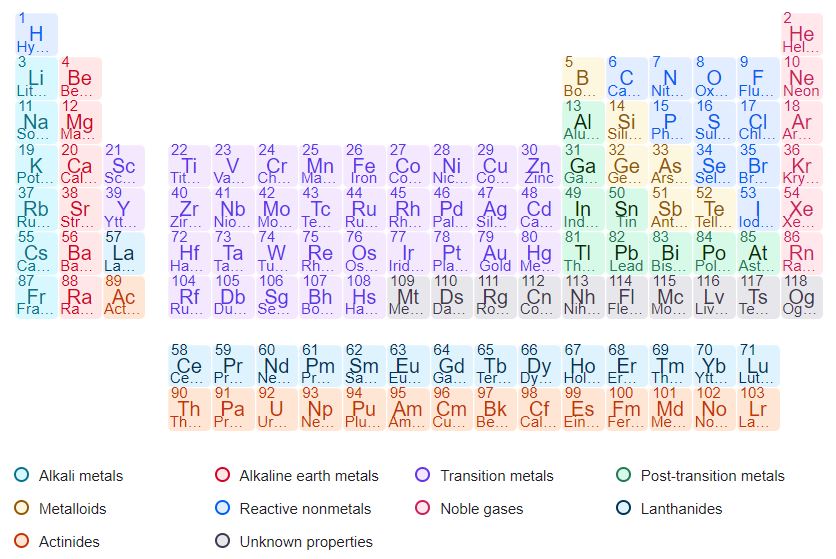
Chapter 1
物质的聚集状态
-
理想气体状态方程:
-
Dalton分压定律
- (温度和总体积恒定)
- 物质的量分数:,
- (温度和总压强恒定)
-
相(phase):物理和化学性质完全均匀的部分称为相。
- 气体-一个气相,液体-一、二、三相共存,固体-一个固体一个相
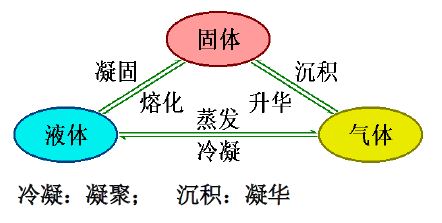
- 气体的液化
- 永久气体:室温下不会液化的气体
- 可凝聚气体:临界温度高于室温
- 液体的蒸发
- 气-液两相达平衡时的压强——饱和蒸汽压
- Clausius-Clapeyron方程
- 凝固和融化
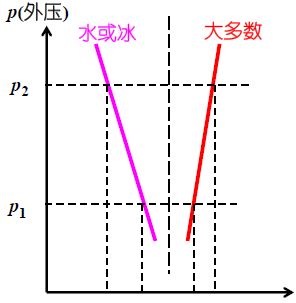
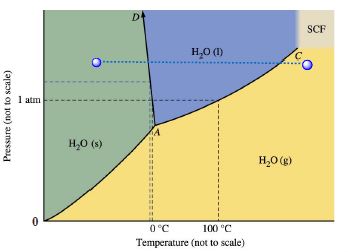
- 水的相图
- AC线不能无限延长
溶液
- 表示浓度的方法
- 质量分数:
- 物质的量分数:
- 质量摩尔浓度:
- 物质的量浓度:
- 溶解度
- ,
- 影响溶解度的因素
- 温度:(温度越高溶解度越小)
- 压强:(亨利定律)
- 非电解质稀溶液的依数性
- 浓度越高蒸气压下降
- Raoult定律:
- 浓度越高沸点升高
- 浓度越高凝固点下降
- 浓度越高蒸气压下降
- 渗透压
Chapter 2
原子的量子力学模型
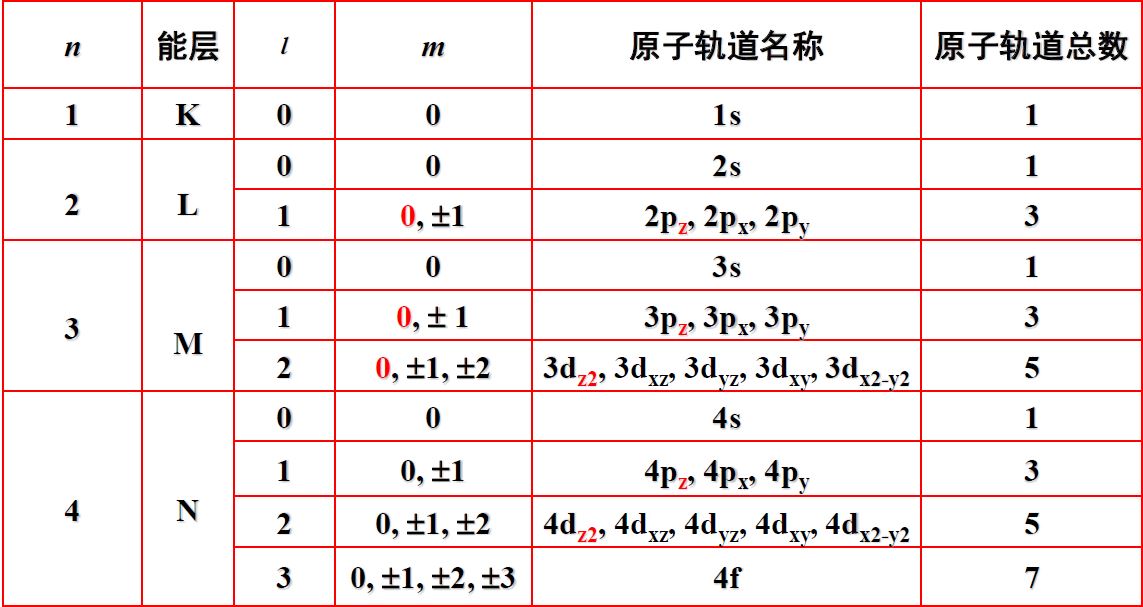
- 径函数,由n, l决定;角函数,由l, m决定。
n为主量子数,n=1, 2, 3, …
l为角量子数,l=0 (s), 1 (p), 2 (d), 3 (f), …, n-1
m为磁量子数,m=0, ±1, ±2, …, ±l
-
对于径函数R(r)
径节面指径函数为零的地方,径节面数=n-l-1
是电子沿径向出现的概率密度
-
对于角函数
只取决于l和m,而与n无关
是电子沿角向出现的概率密度
角节面数=l
总节面数=n-1
-
小结
主量子数n决定电子的能量和电子距离核的远近
角量子数l决定电子轨道的形状
磁量子数m决定角动量的分量大小
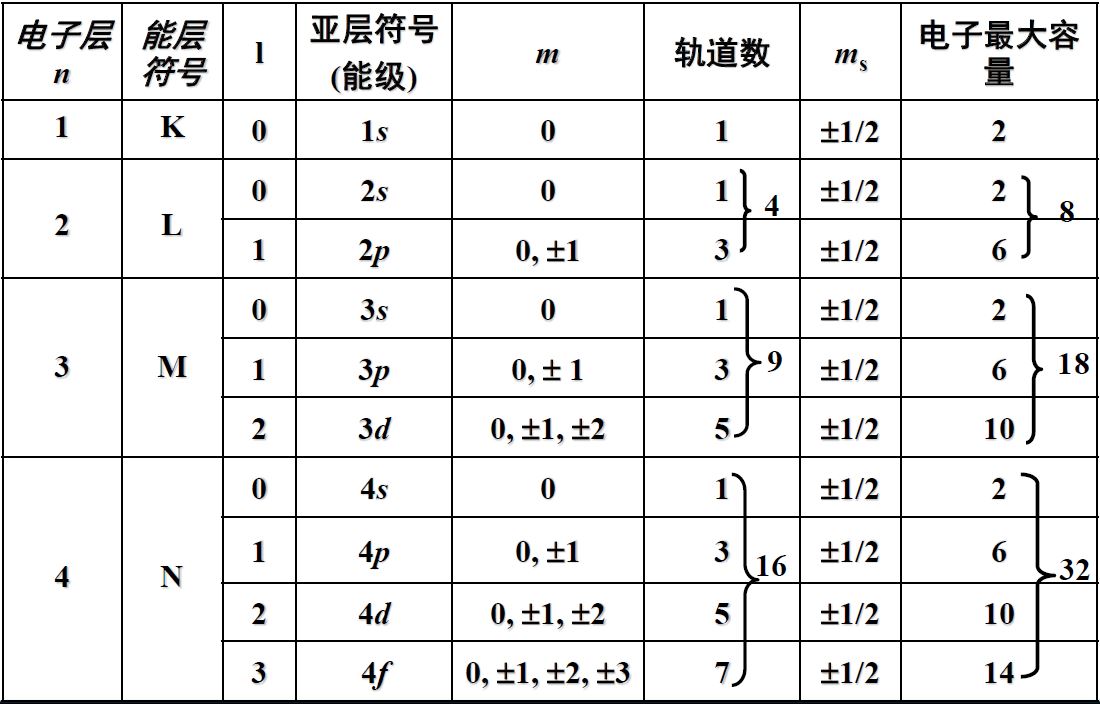
多电子原子结构
基态:原子处于能量最低的状态,电子排布是唯一的
激发态:电子的排布不是唯一的
构造原理:按照核内加一个质子、核外加一个电子的方式逐渐构建原子,新增加的核外电子将按以下顺序陆续填满各个原子轨道。
(1s)(2s2p)(3s3p)(4s3d4p)(5s4d5p)(6s4f5d6p)(7s5f6d7p)
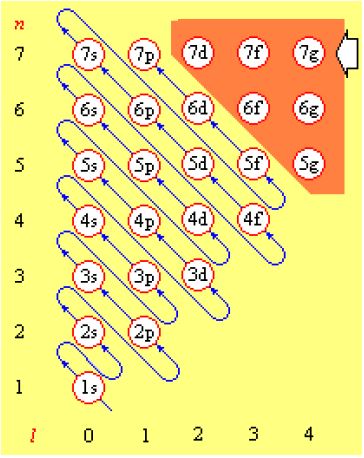
- 排布规则
- 泡利不相容原理——原子中不存在四个量子数完全相同的两个电子,每个轨道最多接纳两个自旋相反的电子
- 能量最低原理——不违反泡利不相容原理的前提下,电子总是先进入能量最低的轨道
- 洪特规则
- 填充主量子数和角量子数相同的各个轨道时,电子总是先按自旋平行的方式占有各个轨道
- 轨道处于半满或全满的状态时,体系能量低
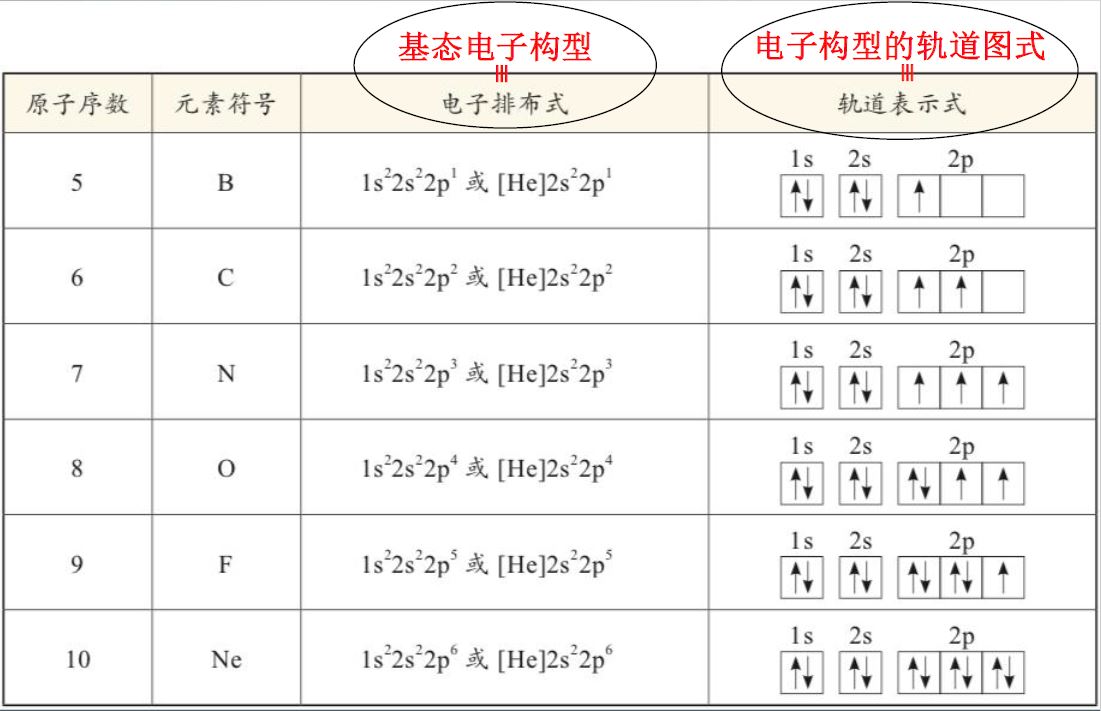
- 顺磁性:具有不成对电子成单电子、不成对电子数越多,原子或离子的顺磁性越大
Chapter 3
3-1 离子键-价键理论-杂化轨道理论-价层电子对互斥理论-2022.pdf
离子键
离子键:原子间通过正、负离子电性吸引的互相作用称为离子键
-
离子键的本质时静电引力(库仑力)
- 离子电荷越大,间距越小,引力越大,离子键越强
- 无方向性、无饱和性
- 电负性差值越大,键的离子性越大
- 阴离子:大球;阳离子:小球
-
离子键的强度
晶格能(U):气态离子形成1mol离子晶体的过程释放的能量
影响因素:离子间距,离子电荷数,晶体类型
晶格能越大,硬度越大,熔点越高
-
离子半径
正离子的离子半径比同一元素的原子半径小
负离子的原子半径比同一元素的原子半径大
-
波恩-哈勃循环
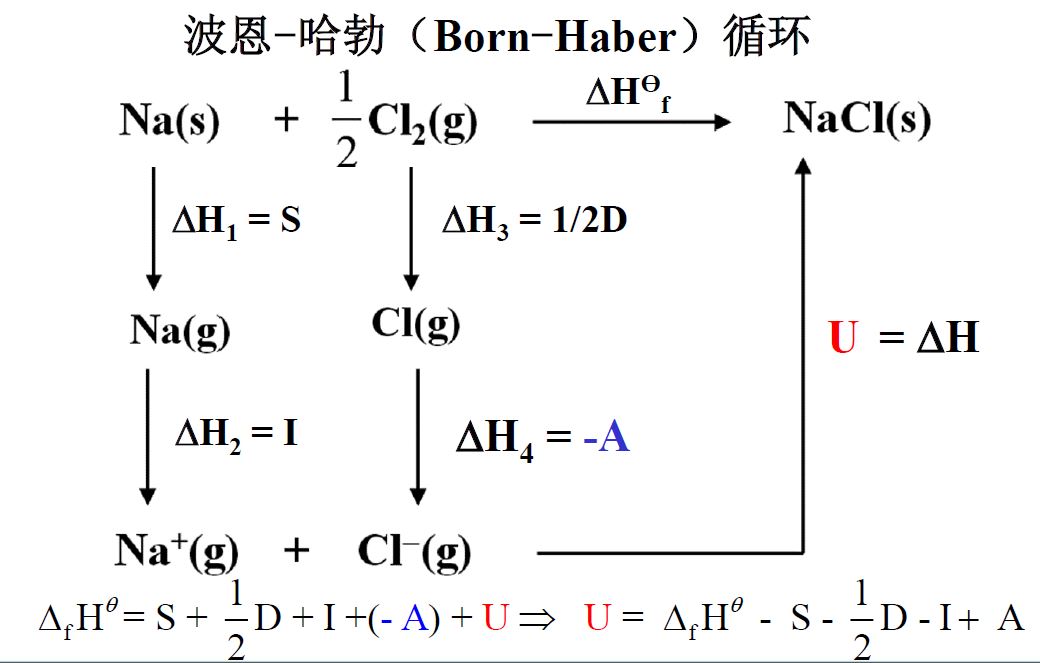
共价键
经典路易斯学说
原子通过共用电子对形成的化学键称为共价键
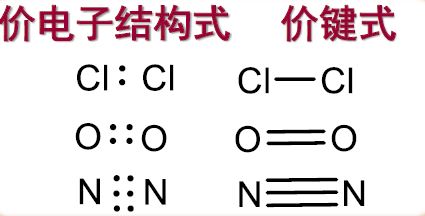
两个成键原子的核间距离称为键长,原子之间的共享电子对数目称为键级
键角:分子中键与键之间的夹角
极性共价键:成键电子对在其中一个原子周围出现几率大的共价键
非极性共价键:没有极性
价键理论
形成共价键的两个必要条件
- 2个原子的夹层轨道上有不成对电子,自旋相反
- 2个原子轨道必须有最大程度的重叠
共价键的本质:原子相互接近时轨道重叠,原子通过共用电子对使能量降低而成键
共价键的特点:饱和性(不成对电子用完了,就不能再形成共价键)和方向性(形成的共价键会有一定的角度)
共价键的类型:
- 键:头碰头
- 键:肩并肩,没有键稳定
简单的价键理论不能解释分子的空间构型
杂化轨道理论
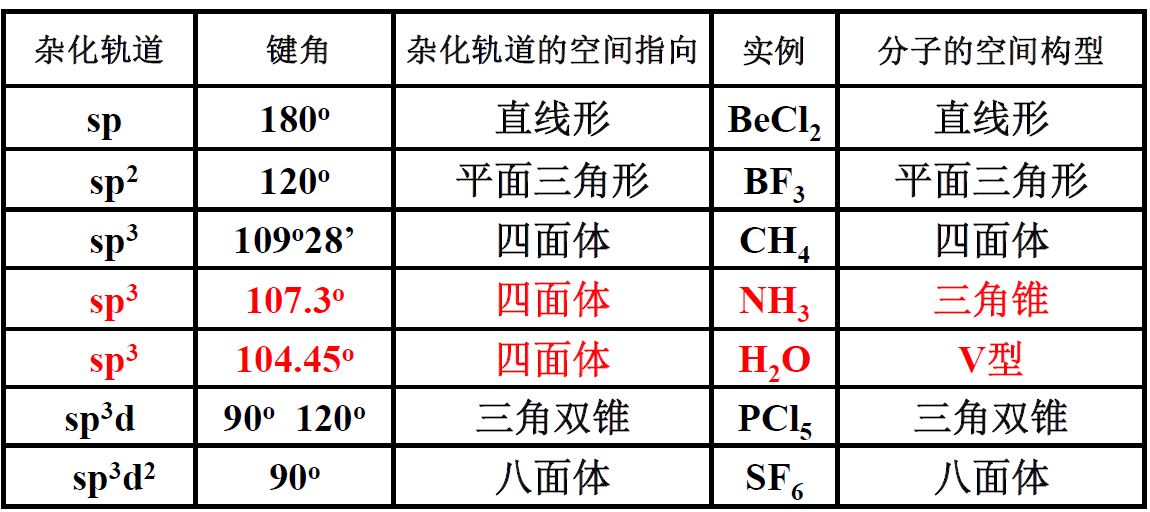
需要掌握外轨型杂化轨道
- 杂化轨道:两个杂化轨道互成180° ,直线型(激发-杂化)
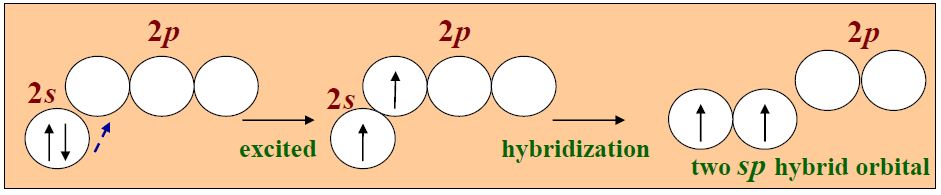
- 杂化轨道:1个ns轨道和2个np轨道组成三个杂化轨道,夹角为120°,平面三角形
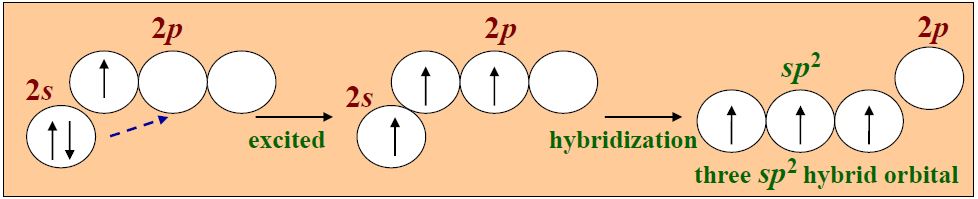
- 杂化轨道:1个ns轨道和3个np轨道组成四个杂化轨道,夹角为109°28‘,四面体

- 杂化轨道:1个ns轨道、3个np轨道和1个nd轨道组合成5个能量相等的杂化轨道,夹角为90°、120°,三角双锥
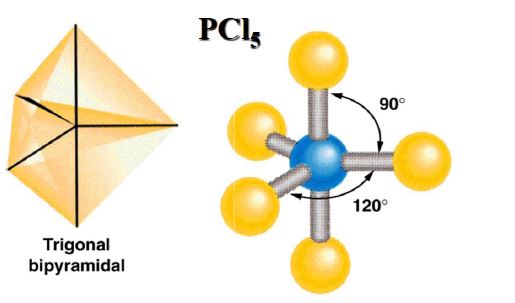
-
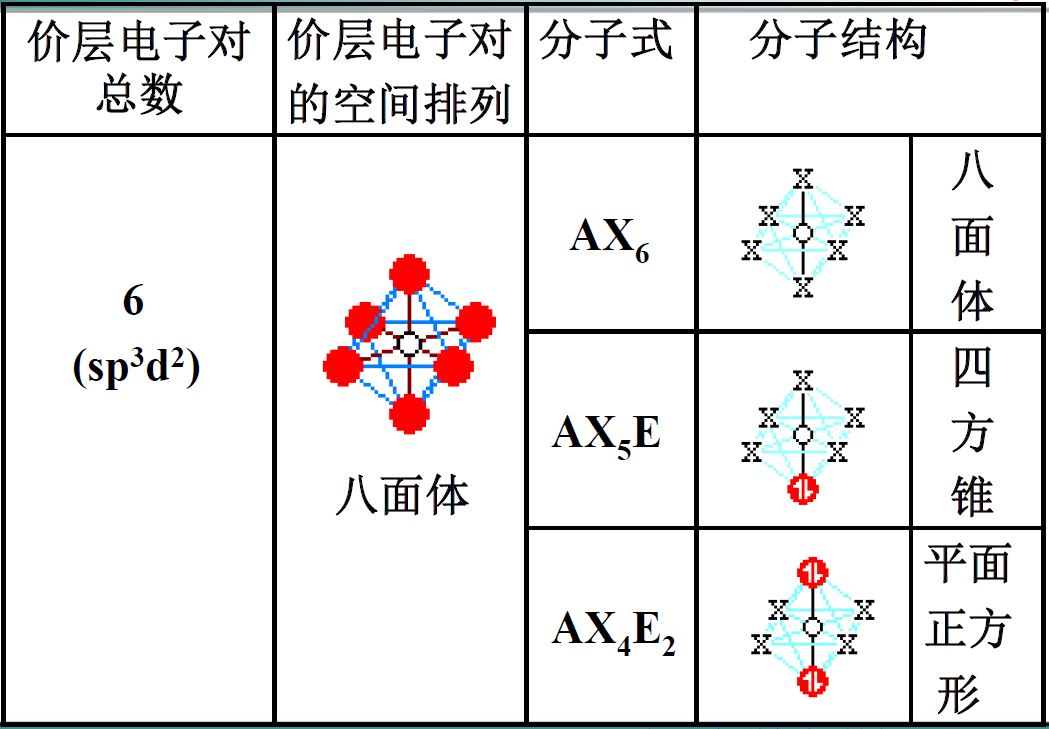
杂化轨道:1个ns轨道、3个np轨道和2个nd轨道组成6个能量相等的杂化轨道,夹角为90°,八面体
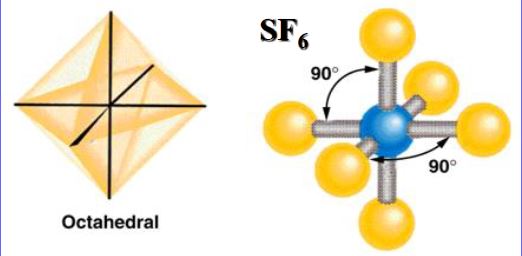
-
乙烯分子:一个键,一个键
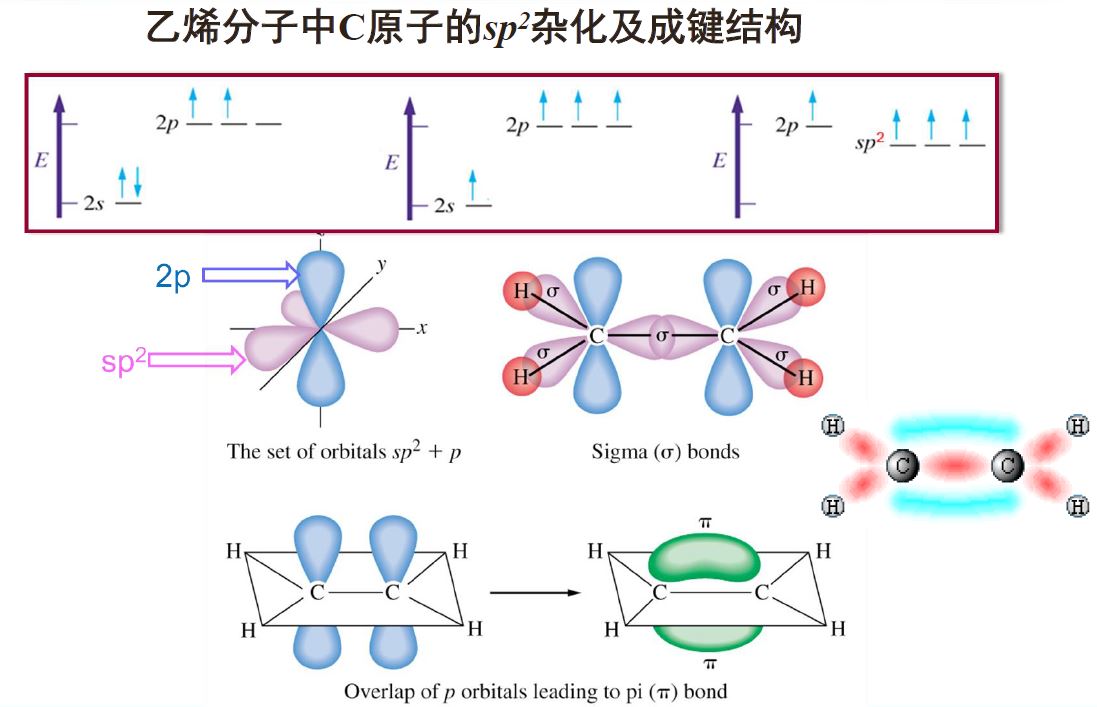
乙炔分子:一个键,两个键
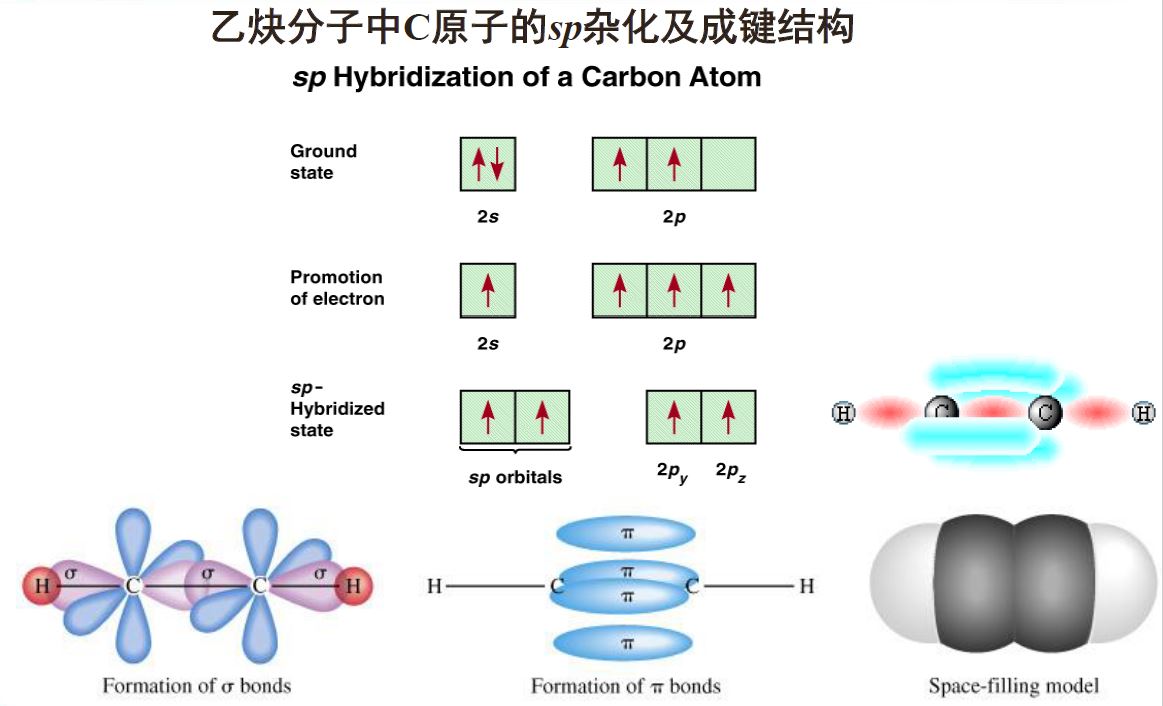
- 杂化轨道随着s成分的增加键能增大键长减小
- 杂化轨道分为等性(成键)和不等性(成键+孤对电子)杂化轨道两种
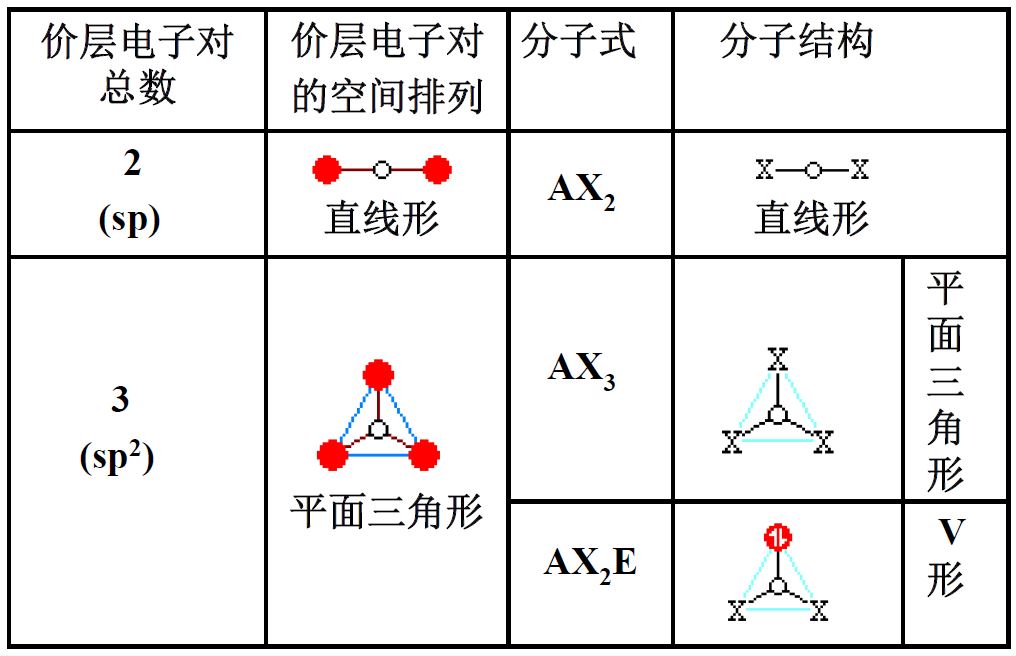
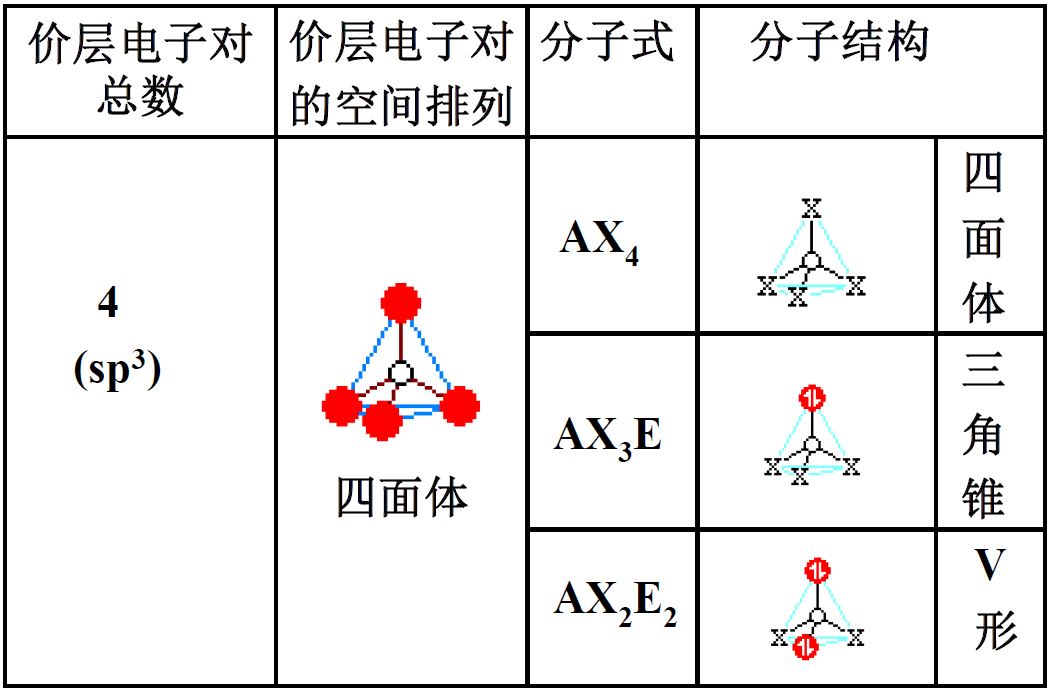
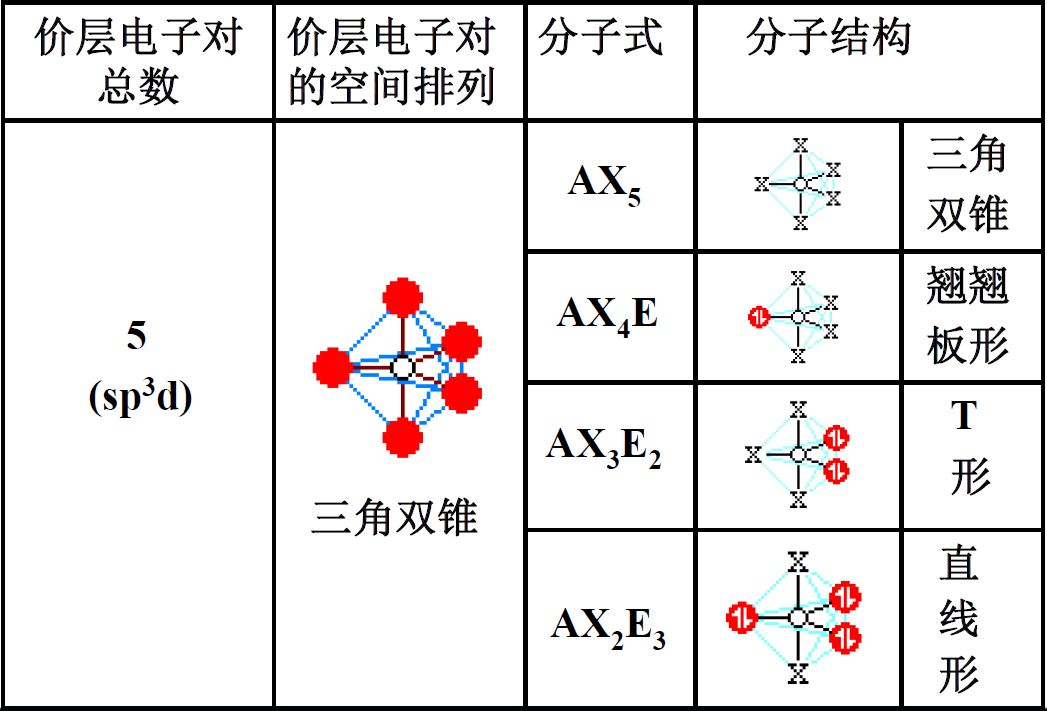
价层电子对互斥理论(VSEPR)
- 价层电子对=成键电子对+价层孤对电子
- 分子的空间构型仅取决于价层电子对中的成键电子对的空间位置
- 排斥力
- 孤电子对对孤电子对>孤电子对对成对电子对>成键电子对对成键电子对
- 90°>120°>180°
- 中心原子电负性越大,成键电子对排斥越大
- 配位原子电负性越大,成键电子对排斥越小
- 多键对多键>多键对单键>单键对单键
- 中心原子的价电子对数
- O,S,Se,Te作为配位原子不计数
- 形成双键-1,形成三键-2
- 1.5->2,2.5->3
分子轨道理论
- 要点
- 分子中,电子不再属于单个原子
- 分子轨道近似由原子轨道线性组合形成
- 满足
- 泡利原理:每个轨道最多容纳2个自旋相反的电子
- 能量最低原理:能量较低的轨道填满之后,才能填入能量较高的轨道
- 洪特规则:当电子填入2个以上等能量轨道时,电子总是先以自旋相同的方式占据这些轨道直到半充满。
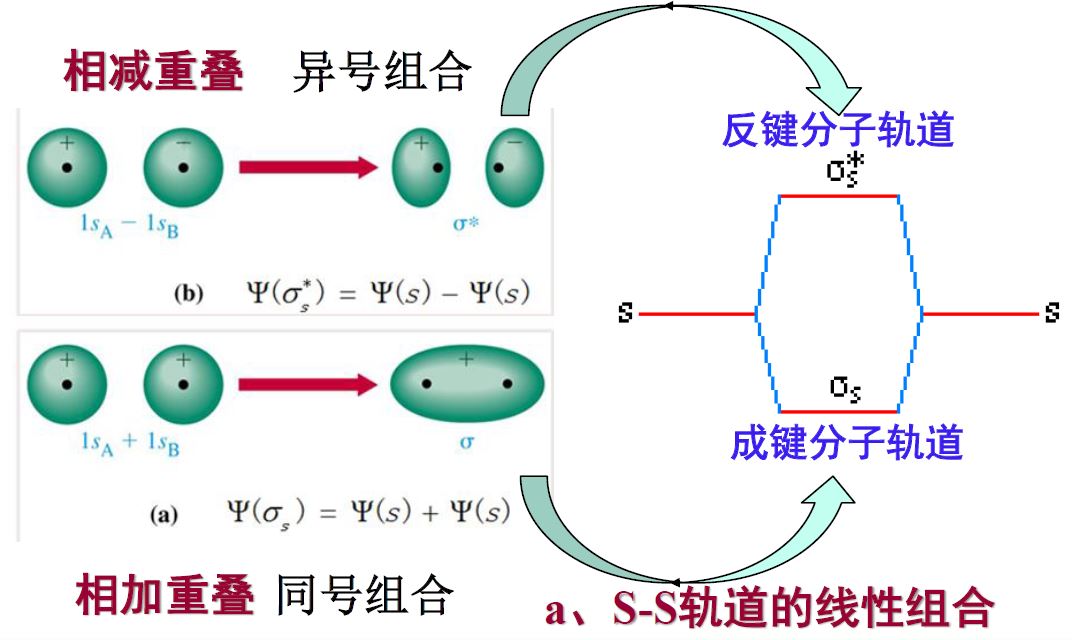
- 两个原子的原子轨道线性组合形成两个分子轨道
- 成键分子轨道:能量低,电子云密度大
- 反键电子轨道:能量高,电子云密度为零
- 波函数叠加,相位相同波增强,能量降低。
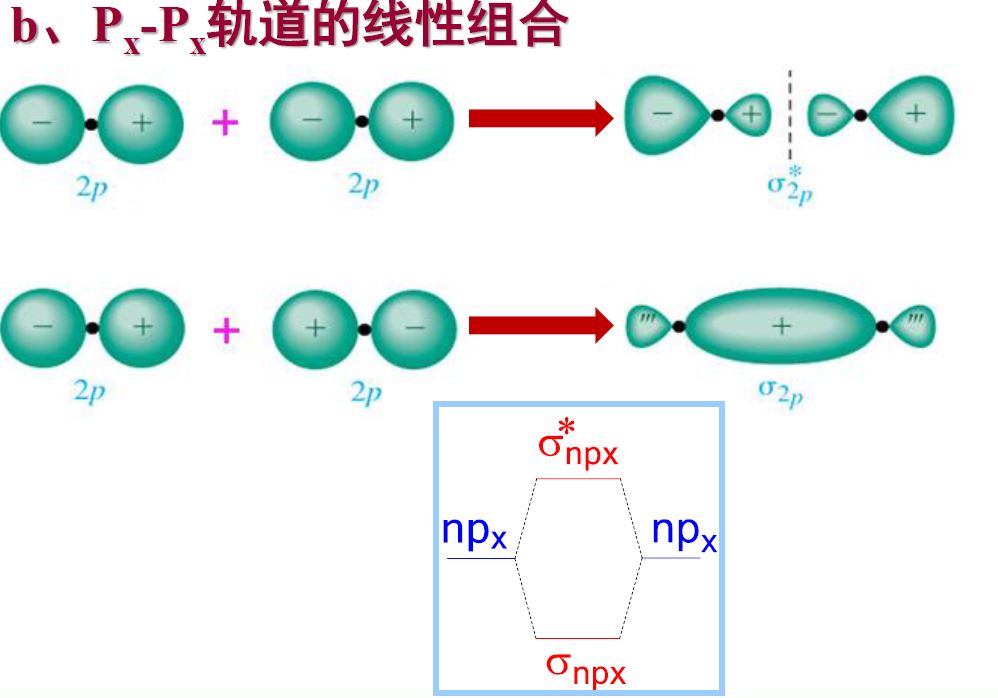
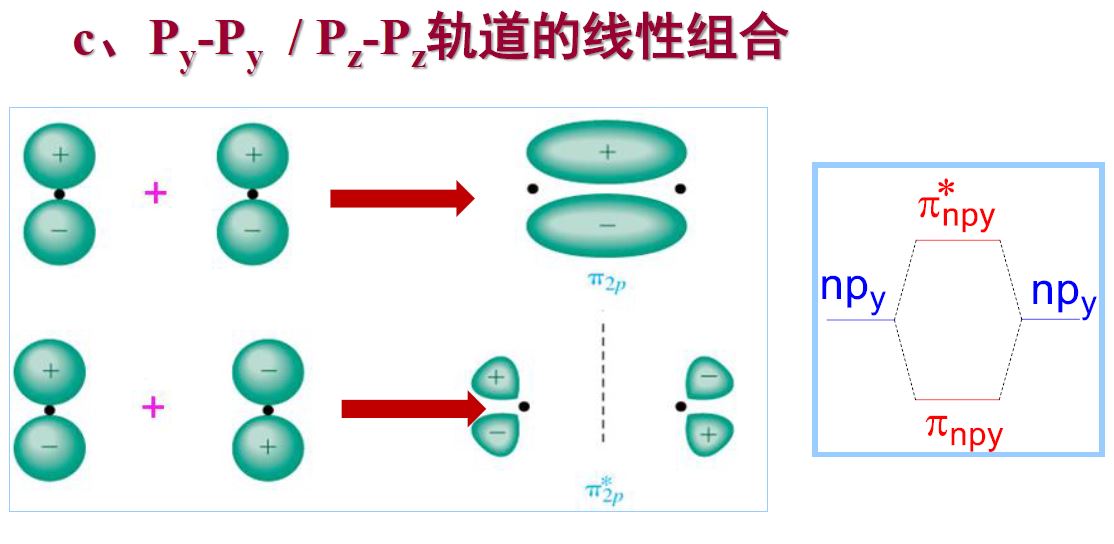
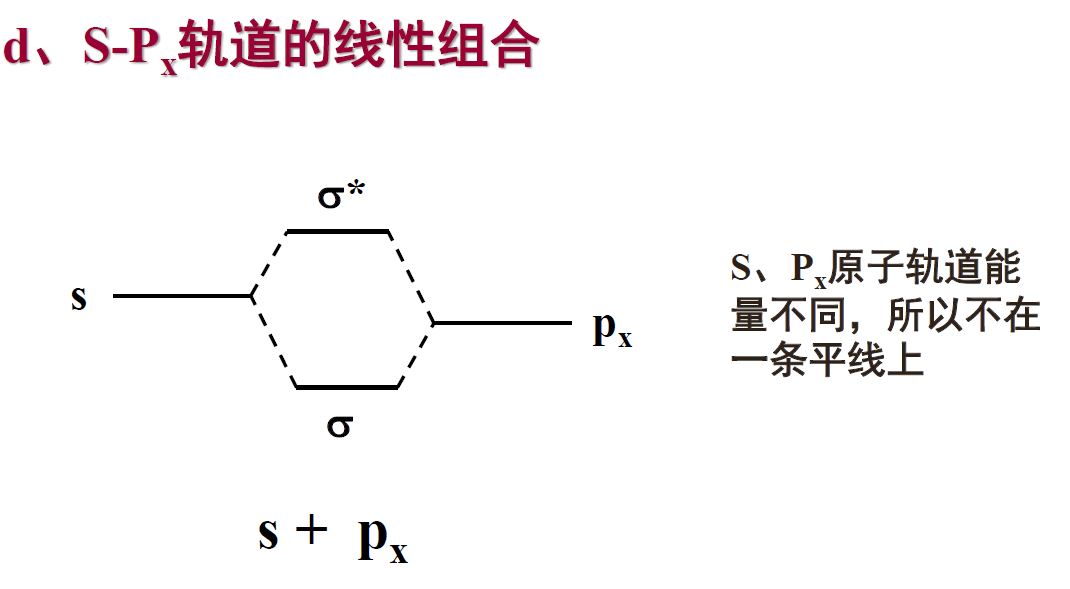
- 原子轨道线性组合的原则
- 能量匹配原则:只有能量相近的原子轨道之间可以进行线性组合
- 对称性匹配原则
- 对称轨道:s-s,px-px (轨道)
- 反对称轨道:px-py (轨道)
- 最大重叠原则
- 键级=
- 键级越高,键能越大,键长越短
- 同核双原子分子
- 有单电子,有顺磁性
- 键级不是0,就能稳定存在
- 详见ppt
分子间作用力
-
分子与分子之间存在一种比化学键弱得多的相互作用力
- 短程作用,对距离非常敏感
- 无方向性和饱和性
-
分子的极性
- 同核双原子分子:非极性键
- 异核双原子分子:极性键
- 结构对称的多原子分子,键有极性,分子没有极性
-
分子间作用力
- 取向力(刻松力)
- 极性分子与极性分子之间的作用力
- 诱导力(德拜力)
- 极性分子与非极性分子之间的作用力,使非极性分子有极性
- 极性分子与极性分子之间也会有
- 色散力(伦敦力)
- 核外电子不断运动的过程中产生的正负电荷重心分离,产生瞬时偶极
- 氢键
- 存在于分子之间和分子之内的作用力
- 分子中与高电负性原子X以共价键相连的H原子与另一分子中一个高电负性原子Y之间形成的弱键
- N、O、F的氢化物分子
- 氢键的强弱与X,Y的电负性与大小密切相关
- 分子内氢键降低沸点,分子间氢键升高沸点
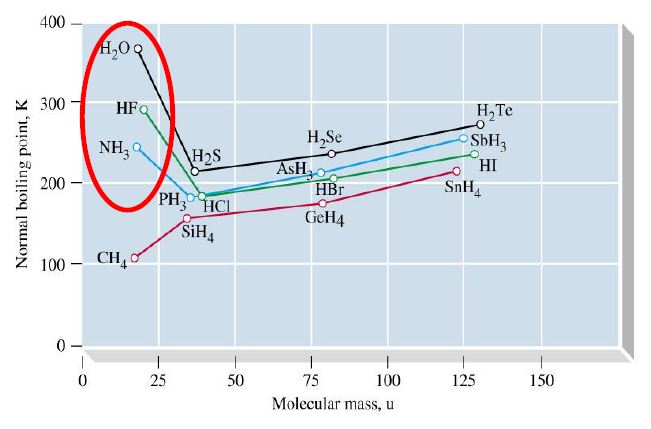
- 大部分分子间作用力以色散力为主
- 非极性分子,分子间色散力随分子量增加而加强
- 稀有气体,水分子与稀有气体间的诱导力随分子量增加而增大
- 取向力(刻松力)
Chapter 4
热力学第一定律
-
体系:指研究的对象,包含一定种类和数量的物质
-
环境:在体系之外,与体系密切相关的部分
-
体系分类
- 敞开体系:能量+物质
- 封闭体系:能量
- 孤立体系:无交换
-
状态:体系所有物理性质和化学性质的综合表现
- 始态
- 终态
-
状态函数
- 内能U、焓H、熵S、自由能G
- 广延性质:有加和性
- 强度性质:与物质的量无关
-
过程与途径
- 过程:体系的状态随时间发生变化
- 途径:体系变化过程中具体经历的状态
-
热力学第一定律:能量守恒定律
,w-功(+:环境->体系),q-热(+:环境->体系)
-
体积功的计算
- 膨胀功:
- 可逆过程和最大功
- 压缩功(压缩次数越多,环境对体系做功越小)
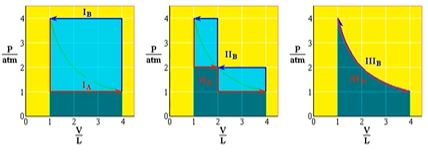
- 可逆过程
- 相变点发生相变
热化学
- 恒容热效应
- ,
- 恒压热效应
- 焓与焓变
- 定义:
- 如果只有固态和液态的反应,较小,
- 热容
- 比热容:,摩尔热容:
- :摩尔恒容热容,:摩尔恒压热容
- 单原子分子理想气体:,
- 双原子分子理想气体:,
- ,
- 盖斯定律
复习